LANJUTAN SOA; DAN PEMBAHASAN SEGITIGA DAN SEGI EMPAT

Simak kumpulan soal UN dengan materi segiempat dan segitiga pada pembahasan di bawah.

Contoh 1: Soal UN Matematika SMP/MTs Tahun 2019

Pak Burhan membuat taman berbentuk persegi panjang berukuran 5 m × 4 m. Di tengah taman dibuat kolam berbentuk lingkaran diameter 2,8 m. Taman di luar kolam tersebut ditanami rumput. Luas taman yang ditanami rumput adalah ….
A. 6,16 m2
B. 7,68 m2
C. 12,32 m2
D. 13,84 m2

Pembahasan:

Luas taman = p × l
= 5 m × 4 m
= 20 m2

Luas kolam berbentuk lingkaran

$= \pi \times r^{2}$

$= \frac{22}{7} \times \frac{2,8}{2} \times \frac{2,8}{2}$

$= \frac{22}{7} \times 1,4 \times 1,4$

$= \frac{22}{7} \times 1,96$

$= 6,16 \; m^{2}$

Luas taman yang ditanami rumput = 20 m2 – 6,16 m2 = 13,84 m2

Jawaban: D

Contoh 2: Soal UN MATEMATIKA SMP/MTs 2013

Sebidang kebun berbentuk persegipanjang berukuran 100 m x 80 m. Di sekeliling kebun akan ditanam pohon dengan jarak 10 m antar pohon. Banyak pohon yang diperlukan adalah ….

A. 36 pohon

B. 46 pohon

C. 72 pohon

D. 180 pohon

Pembahasan:

Mencari keliling persegi panjang:

$K = 2 \left( p + l \right)$

$K = 2 \left( 100 + 80 \right)$

$K = 2 \times 180$

$K = 360 \; \textrm{m}$

Mencari banyak pohon yang diperlukan:

$= \frac{360}{10}$

$= 36 \; \textrm{[pohon}$

Jawaban: A

Contoh 3: Soal UN MATEMATIKA SMP/MTs 2012

Pak Rahman mempunyai sebidang tanah berbentuk persegi panjang dengan ukuran 30 m x 25 m. Tanah tersebut dipagari kawat sebanyak tiga kali lilitan. Panjang minimal kawat yang dibutuhkan adalah ….

A. 110 m

B. 330 m

C. 440 m

D. 750 m

Pembahasan:

Mencari keliling bidang tanah yang akan dipagari kawat:

$K = 2 \left( p + l \right)$

$K = 2 \left( 30 + 25 \right)$

$K = 2 \left( 55 \right)$

$K = 110 \; \textrm{cm}$

Panjang kawat untuk mengelilingi bidang tanah sebanyak tiga kali lilitan:

$= 3 \times 110$

$= 330 \; \textrm{cm}$

Jawaban: B

Contoh 4: Soal UN MATEMATIKA SMP/MTs 2011

Pak Ali mempunyai kebun dengan bentuk seperti pada gambar di bawah.

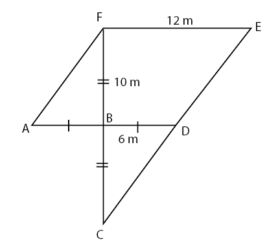
Kebun tersebut akan dijual dengan harga Rp200.000,00 per m2. Hasil penjualan kebun Pak Ali adalah ….

A. Rp28.800.000,00

B. Rp30.000.000,00

C. Rp36.000.000,00

D. Rp57.600.000,00

Pembahasan:

Gambar pada soal disusun oleh jajar genjang dan segitiga seperti terlihat pada gambar di bawah.

Mencari luas jajar genjang:

$L_{1} = a \times t$

$L_{1} = 12 \times 10$

$L_{1} = 120 \; \textrm{m}^{2}$

Mencari luas segitiga:

$L_{2} = \frac{1}{2} \times 6 \times 10$

$L_{2} = \frac{1}{2} \times 60$

$L_{2} = 30$

Jadi, luas gabungan dua bangun tersebut adalah

$L = L_{1} + L_{2}$

$L = 120 + 30$

$L = 150 \; cm^{2}$

Hasil penjualan kebun Pak Ali:

$= 150 \times Rp200.000,00$

$= Rp30.000.000,00$

Jawaban: B

Contoh 5: Soal UN MATEMATIKA SMP/MTs Tahun 2010

Perhatikan gambar!

Daerah yang diarsir adalah sketsa tanah yang ditanami rumput. Luas hamparan rumput tersebut adalah ….

A. 2.400 m2

B. 1.900 m2

C. 1.400 m2

D. 1.200 m2

Pembahasan:

Luas bangun yang diberikan pada soal dapat diperoleh dari luas trapesium siku-siku dikurangi luas persegi panjang kecil, seperti terlihat pada gambar di bawah.

Mencari luas trapesium siku-siku:

$L_{1} = \frac{\textrm{jumlah sisi sejajar} \times t }{2}$

$= \frac{ \left( 45 + 75 \right) \times 40 }{2}$

$= \frac{ 120 \times 40 }{2}$

$= 2.400 \; \textrm{cm}^{2}$

Luas persegi panjang kecil adalah L2, maka

$L_{2} = p \times l$

$= 25 \times 20$

$= 500 \; \textrm{cm}^{2}$

Luas hamparan rumput tersebut adalah

$= 2.400 - 500$

$= 1.900 \; \textrm{cm}^{2}$

Jawaban: B

Contoh 6: Soal UN MATEMATIKA SMP/MTs Tahun 2010

Perhatikan gambar!

Luas daerah bangun pada gambar di atas adalah ….

A. 133 cm2

B. 138 cm2

C. 162 cm2

D. 181 cm2

Pembahasan:

Gambar yang diberikan pada soal dibangun oleh persegi panjang dikurang luas trapesium, seperti yang terlihat pada gambar di bawah.

Mencari luas persegi panjang:

$L_{p} = P \times l$

$L_{p} = 19 \times 14$

$L_{p} = 266 \; cm^{2}$

Mencari luas trapesium:

$L_{t} = \frac{\textrm{jumlah sisi sejajar} \times t}{2}$

$L_{t} = \frac{ \left( 19 + 7 \right) \times 8}{2}$

$L_{t} = \frac{ 26 \times 8}{2}$

$L_{t} = 104 \; cm^{2}$

Luas daerah bangun pada gambar di atas:

$= 266 - 104$

$= 162 \; cm^{2}$

Jawaban: C

Contoh 7: Soal UN MATEMATIKA SMP/MTs Tahun 2006

Taman berbentuk trapesium sama kaki dengan panjang sisi-sisi sejajarnya (x + 4) m dan (3x + 2) m. Jika jarak kedua garis sejajar 2x m dan luas taman 180 m2, keliling taman adalah ….

A. 54 m

B. 56 m

C. 65 m

D. 69 m

Pembahasan:

Diketahui:

Sisi sejajar pertama trapesium = x + 4

Sisi sejajar kedua trapesium = 3x + 2

Tinggi trapesium = 2x

Bentuknya dapat dilihat seperti gambar di bawah.

Luas trapesium adalah

$L = \frac{ \textrm{jumlah sisi sejajar} \times t}{2}$

$180 = \frac{ \left( x + 4 + 3x + 2 \right) \times 2x}{2}$

$2 \times 180 = \left( x + 4 + 3x + 2 \right) \times 2x$

$360 = \left( 4x + 6 \right) \times 2x$

$360 = 8x^{2} + 12x$

$8x^{2} + 12x - 360 = 0$

$2x^{2} + 3x - 90 = 0$

Untuk mendapatkan nilai x, maka kita perlu menyelesaikan persamaan kuadrat di atas.

$2x^{2} + 3x - 90 = 0$

$2x^{2} - 12x + 15x - 90 = 0$

$2x \left( x - 6\right) + 15 \left( x - 6 \right) = 0$

$\left( 2x + 15 \right) \left( x - 6 \right) = 0$

$2x + 15 = 0 \; \textrm{atau} \; x - 6 = 0$

Sehingga diperoleh,

$2x + 15 = 0 \rightarrow x = - \frac{15}{2}$

$x - 6 = 0 \rightarrow x = 6$

Pilih nilai x = 6 karena tidak ada panjang yang nilainya negatif. Sehingga diperoleh ukuran masing-masing sisi trapesium seperti berikut.

Sisi sejajar 1 trapesium:

$= x + 4$

$= 6 + 4$

$= 10 \; \textrm{m}$

Sisi sejajar 2 trapesium:

$= 3x + 2$

$= 3(6) + 2$

$= 18 + 2$

$= 20 \; \textrm{m}$

Tinggi trapesium:

$= 2x$

$= 2 \times 6$

$= 12 \; m$

Ukuran dalam gambar dapat dilihat seperti berikut.

Untuk menghitung keliling, kita perlu menghitung sisi miring dari trapesium tersebut terlebih dahulu. Panjang sisi miring trapesium adalah:

$= \sqrt{12^{2} + 5^{2}}$

$= \sqrt{144 + 25}$

$= \sqrt{169}$

$= 13 \; \textrm{m}$

Keliling trapesium:

$= 10 + 13 + 20 + 13$

$= 56 \; \textrm{m}$

Jawaban: B

Bagaimana contoh soal dan pembahasan soal UN untuk materi segitiga dan segi empat, mudah bukan? Terimakasih sudah mengunjungi idschool.net, semoga bermanfaat!!